크루스칼 알고리즘
코딩 테스트 문제를 풀다보면 마주치게 되는 크루스칼 알고리즘에 대해 알아봤다.
What is Kruskal’s algorithm?
최소 비용 신장 부분 트리를 찾는 알고리즘
변의 개수를 E, 꼭짓점의 개수를 V라고 하면 이 알고리즘의 시간복잡도는 O(ElogV)
노드와 간선으로 이루어진 그래프가 있을 때, 가장 적은 비용으로 노드를 연결하는 방법을 찾는 알고리즘이다.
주로 간선마다 가중치가 있을 때 가장 적은 비용으로 연결하기 위해 사용한다.
How it works
위키백과의 크루스칼 알고리즘 예제를 통해 어떻게 동작하는지 알아보자.
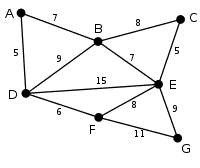
간선 옆에 있는 숫자는 변의 가중치를 가리킨다.
지금은 모든 간선의 색이 검정색이다.
앞으로 연결된 선은 녹색으로, 연결할 수 없는 선은 빨강으로 나타낸다.
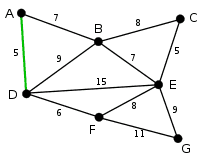
가중치가 가장 작은 간선을 고른다.
지금처럼 가중치가 가장 작은 선이 두개을 경우 아무거나 골라 선택하면 된다.
AD 와 CE 중 AD를 선택하고, AD는 연결된 선이기 때문에 녹색으로 변경한다.
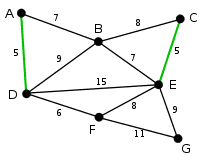
나머지 간선 중 가중치가 가장 작은 CE를 선택한다.
loop를 만들지 않는 선이니까 연결할 수 있다. 녹색으로 바꿔준다.
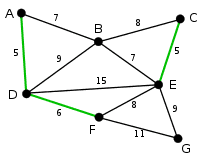
같은 방식으로 가중치가 6인 DF를 선택한다.
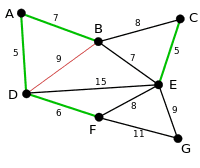
다음으로 가중치가 작은 간선인 AB와 BE 중 임의로 AB를 고른다.
AB를 연결하기로 결정하면 BD는 loop를 만드는 선이므로 연결할 수 없는 선이 된다.
만약 AB가 아닌 BE를 연결하기로 결정했다면 AB가 연결할 수 없는 선이 된다.
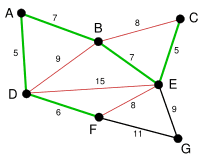
다음으로 가중치가 작은 BE를 연결하면 BC, DE, FE가 연결할 수 없는 선이 된다.
BCE 루프를 생성하기 때문에 BC가 빨강색으로 변하고, DEBA 루프를 생성하기 때문에 DE가 빨강색으로 변하고, FEBAD 고리를 생성하기 때문에 FE가 빨강색으로 변한다.
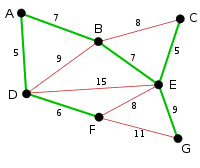
남은 간선 중 가중치가 작은 EG를 연결하고 나면 FG가 연결할 수 없는 선이 되면서 알고리즘이 끝난다.
이렇게 최소 비용 신장 부분 그래프가 완성됐다.
How to apply
이런 크루스칼 알고리즘을 직접 구현하려면 어떻게 해야 될까?
위 예제를 통해 알아봤을 때 크루스칼 알고리즘 구현의 핵심은 다음과 같다고 생각한다.
- 연결할 수 있는 선들 중 가중치가 작은 선 먼저 연결하기
→ 선의 연결여부를 판단할 수 있도록 구현 - 선을 연결했을 때 loop(cycle)이 형성되는지 판단하기
→ 각 노드의 부모를 저장해서 연결될 때마다 부모를 최솟값으로 갱신
1번의 선의 연결여부를 판단하는 코드는 알고리즘을 적용할 문제에 따라 다르게 구현하고, 2번의 cycle이 형성되는지 판단하는 코드는 각 노드의 부모를 나타내는 배열을 만들고 간선들을 최소 비용으로 연결할 때마다 두 노드의 부모 중 최솟값으로 갱신해주도록 구현했다.
이렇게 하면 두 노드의 부모가 같다면 연결했을 때 cycle이 생기는 것을 알 수 있다.
또, 모든 노드가 연결 가능하다면 알고리즘이 끝났을 때 모든 노드의 부모가 하나로 통일된다.